SLRA: Software for weighted structured low-rank approximation

Overview

SLRA is a C software with interface to MATLAB, Octave, and R for solving low-rank approximation problems

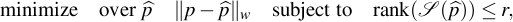
$text{minimize} quad text{over} widehat p quad |p - widehat p|_w quad text{subject to} quad text{rank}({cal S}(widehat p)) leq r,$

with the following features:

mosaic Hankel structured approximating matrix ,
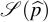weighted 2-norm approximation criterion

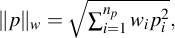
$|p|_w = textstylesqrt{sum_{i=1}^{n_p} w_i p_i^2},$

fixed elements in the approximating matrix,
missing elements in the data matrix,
linear constraints on an approximating matrix's left kernel basis.

For an 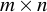mtimes n matrix 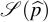{cal S}(widehat p) , with 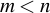m < n , the computational complexity of the cost function and derivative evaluation is 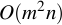O(m^2n) , so that the package is suitable for applications with 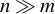ngg m . Problems with 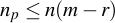n_p leq n(m - r) can not be solved by the method, used in the software.

Usage

In MATLAB/Octave, once the structure and approximation criterion are specified in a variable s (see examples and the manual), the problem is solved by a call of the slra function:

[ph, info] = slra(p, s, r, opt);

The optional parameter opt is used to specify an initial approximation and options for the optimization method.
The output parameter info contains information about the convergence of the optimization method.

System identification

A major application area of mosaic Hankel structured low-rank approximation methods is system identification. The slra package includes a wrapper function ident for identification of linear time-invariant systems. For details see the ident package.

Download and installation

Latest version

Download ZIP File
Download TAR Ball
View on GitHub

Installation

For MATLAB/Octave users: unpack the archive and use addpath in MATLAB/Octave
For R users (Linux): unpack the archive and run make R in console

For advanced users/developers

The instructions how to compile from source are contained here

Citing

@Article{slra-software,
  author = 	 {I. Markovsky and K. Usevich},
  title = 	 {Software for weighted structured low-rank approximation},
  journal =      {J. Comput. Appl. Math.},
  volume =       {256},
  pages =        {278--292},
  year = 	 {2014},
}